欧美高科技国家于250年前就发生组配不顺利，十九世纪中叶，美国最先发明出公差概念并大幅改善组装效率，到二十世纪初美国早已颁布国家级规範(具理论基础、工程实务经验与公信力)，并运用于军品商品生产，成就第一、二、三次工业革命，自动化生产、大量产製与降低成本，提升生活品质，造福人类。吾人急需迎头赶上，了解其原理加以活用，必有生存发展空间。

一.累积公差分析

　　零件经由製作设备加工机具要求每件形状尺寸均达一样，严格来看，每件尺寸皆一样，难度极高，不仅费时亦无必要，因可能须採用更高级精準度之机具，设备费更高，且必需经过筛选才有可能得到，因製作加工过程必产生些微误差，故如何给予合理误差範围是一个严肃课题。宛如轴承之钢珠製作，大量生产后，最严格筛选尺寸与形状类为航空级用，数量虽极少但价格极昂贵，次级品为汽机车用，最后为自行车用，因应功能需求(运转速度)不一样。

　　累积公差(Tolerance Stack-up)产生之因素有(1)加工工具使用一付夹具于表面之施力变异，在同一台工具机装置夹具之变异，加工刀具之磨耗等因素。(2)材料、材质不均匀、内应力释放及表面尺寸之变异等因素。(3)工作人为组装不当及工序操作不当之因素。(4)设备、机构运行之重複性、刚度及运转参数变异(进给、转速等)。(5)环境温溼度对机具与零件尺寸影响之变异，尤其检测室要求精密受测件须于4小时前置入检测室之规定，期盼零件与检测仪具同温，消除温度影响因素。对策为减少装置之数量、严谨之製程管制、环境条件控制、改善材料品质及操作训练。

　　产品组立装配线上如遇到零件或组件无法顺利进行组配，立即影响后续功能测试与交货时程，问题马上直达专案主管并立案管考，产线负责主管及核心干部立刻绷紧神经全力面对，找问题并加以克服，力保恢复产线正常，事后做详细检讨报告避免下次重複出现。

　　长时间观察统计分析，大多归结于製作设计图面标注欠缺周延与不合理，最常出现之原因为下列因素：(1)零件欠互换性设计思考。(2)欠缺基準标注或不明确。(3)累积公差各自解读，纷争不断。(4)忽视未注公差真正值或误解。(5)传统尺寸公差标注之缺陷。(6)不知零件几何形状误差。(7)表面粗度因素。(8)表面处理厚度。(9)忽视合理组装间隙因子。(10)浪费主管与组织专案MRB(Material Review Board)资源。

　　因製作部门一定需按照图面尺寸製作，且精度并需落于公差範围内才会卸下机具，检验部门必须按照图面尺寸及公差检测才可验收放行入库，这两部门工作内容无从影响后续组配顺利与否，甚至于每件皆经功能量规检验，到产线仍发生组配不顺之事，演变成部门间信心问题，连同其他问题，新仇旧恨纠葛在一齐，问题更複杂化。高阶主管与专案主管陷入迅速召集设计、组配产线等相关干部举行特别裁示会议或开MRB会议，共商解决之道，最终裁示拒收或合用(非合格)，然次数一多，高阶主管均心惊胆跳，寝食难安，祈祷品质无缺点。

(1)尺寸公差之侷限

　　近百年来传统习用尺寸(公差)无法控制形体之形状、偏转、方位或位置。游标卡尺及分釐卡只接触到特定截面之最大两点(或三点)，很难确认出是否为真圆与真直，及其他诸如弯曲、蜂腰、中广、锥形、偏斜、波浪型、倾斜、扭曲等形状。

(2)基準不明确

　　同样零件不同标注，其累积公差各不相同。如图1为各段之标注尺寸，则XY距离累积最大公差值为26±0.15。

图1.尺寸链标注法(ASME Y14.5M 1994/2009)

　　 下图2各段皆以同一端面作基準线(面)标注尺寸，则XY=26±0.10，比尺寸链标注法小些。

图2.基準线标注法(ASME Y14.5M 1994/2009)

　　如採直接标注尺寸，则没产生累积公差问题，XY=26±0.05，亦即公差最小(图3)，但对零件整体位置而言，仍产生±0.05之偏移不确定之问题，顾此失彼，尤其组配合件时，可能造成干涉或间隙过大之现象，隐藏后续之问题无穷而不知，因零件检查尺寸符合图面标注合格而被忽略与界面之关係，非有经验之工程师无法看出问题所在。

图3.直接标注法(ASME Y14.5M 1994/2009)

(3)正负座标不合理之缺陷

　　国内机製业习用之传统直角坐标之尺寸标注如图4。

图4. 传统直角坐标

　　近70年为弥补尺寸公差不合理之缺陷而发展之几何公差标注如图5。于尺寸公差下面加一长方框，第一格为几何公差型态，本文选位置公差(正位度)，第二格为几何公差範围，后面加一修饰符号M，意为最大材料条件(Maximum material condition)。

图5. 几何公差标注

　　优劣比较：传统直角坐标之尺寸标注其孔心合格区域仅拘限于0.05之正方形区块而已，孔心合格区(图6)，明显不合理，因点1及点2相对于理想中心均为等距，而点1为合格，点2则不合格(图7)，如以对角线为直径之圆形区块才合理，同时也合理扩增57.1%之区块面积，可大降製作工具模具成本。

 

图6.孔心合格区比较

　　如再用最大材料情况M修饰，可第二度扩增合格区至ψ0.13，或称为红利公差(Bonus tolerance)。

图7. 最大材料情况

　　位置度原则应用时，其公差大小由设计师需要而定，非由座标转换而成，此公差係由外形（孔及配合件）之最大材料尺寸来决定。如上图中，位置度公差ψ0.07㎜为以孔于最大材料尺寸（最小孔径ψ3.97㎜）为準。当孔之尺寸偏离最大材料尺寸时，孔之位置度公差允许超过原来之公差带，于偏转範围内偏转其位置。如ψ0.13㎜增额公差（Bonus tolerance）为孔加工到最高极限尺寸ψ4.03㎜时容许之位置度公差。换言之，几何形状误差可随加工孔径变异而变，变异量为孔径尺寸增加量。

(4)累积误差效应

　　零件因设计图面不够完整，造成设计、製作加工、检测与客户之间之见解分歧，产生之争议不断，严重影响生产、组装效率、功能测试与上市时机，直接影响获利。产品主管虚耗宝贵时间去组织专案找出再现性问题，同样耗损人力、物力、时间，增加成本负担。三星Note 7品质缺陷自燃意外，事后做25万件次之再现性分析，才确认事故原因，可想像过程中相关主管与工程师背负之压力与煎熬，还好有找到原因才能对症下药改进，但所损失之商誉极为庞大。品质是品牌的生命。

二.累积公差解决方案

　　(1)最差状况模式 ，T为公差值直接累加，最差情况为将各零件(各段)之最长尺寸累加，最短尺寸累加，可取得组合件(全段)之长度尺寸範围，但结果为变异数(公差)过长之虞，零件间隙过大，虽可保证后续组装或维修具互换性，但组合件余隙过大，会影响功能规格测试要求，运转件太鬆如同撞击，产生震动、噪音及加速磨耗，同时伴随温度骤升，严重伤害产品寿期，品质不良之设计。

　　(2)统计模式，将各零件公差值自乘，再累加后开平方根，可得绝大多数（99.73％）零件为合格，易製、易验、易组、易维修，工业界快速实用。

　　实务上尺寸精度于生产及检验过程中会产生偶发性、间断性、显着性之变异（机具不同、材质不同、操作者不同、时间不同），而製作加工操作时，均以中间值为目标，如稍有误差属难以避免之正常现象，亦希望能落在公差值内。例如设计图标注双向公差ψ30±0.1 mm，製作现场潜规则均以ψ30 mm为加工目标，因工具机出厂就隐含本身精度误差，后续使用产生机件磨耗误差，加上操作人情绪技术误差，均属不可避免现象，综合交错所产生之总误差期盼落在公差範围内就合格。如故意偏好加工在尺寸上限或下限(特例为车製螺牙情况，以提高防蚀处理膜厚因素之公母配合)，则不合格率比前述骤升一倍。同理;亦适用于单向公差标注，如标注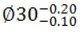 mm，则加工目标就以中值ψ29.85 mm为目标。如设计图标注 mm，则加工目标就以中值ψ30.15 mm为目标。换言之，加工在最长与最短两极端之零件数量其机率很低，故依统计原理计算较合理。

　　其他尚有Spott’s modified model Modified statistical model，mi：第i件之平均值在整个範围移动之比率; Mean shift model，，Tasm=Xmax－Xmin；Xmax＝M＋3D；Xmin＝M－3D；M＝Σmi；D＝（Σσi2）1/2; Moment model; Hybrid model与Monte Carlo model等模式，较偏于理论研究领域，惟仍以统计模型为基础，不适用于产业简单、快速、实用需求性。

　　下图为统计情况则视各零件(各段)随机变异製作，首先将各零件长度变异换成6σ模式，次将组合件(全段)之各零件变异值平方和再开方根，可得组合件之尺寸範围，工程实务上较符合功能需求。兹以下面零件有三阶段尺寸为例，则总尺寸範围如何决定比较合理。

图8. 3阶段零件尺寸链标注

假设  

则其总长

解：

　　(1)最差法：最长为2.5+3.2+2.6=8.3，最短为 2.4+3.0+2.5=7.9，则总长度为  ,公差为0.4。

　　(2)统计法：如赋予每阶段之公差皆为6σ(变异值)，则其总长度之变异值为 ,尺寸链之第一段 6σ1=2.5-2.4=0.1 ,σ1=0.0167 ;同理第二段　6σ2=3.2-3.0=0.2 ,σ2=0.0333 ;第三段为 6σ3=2.6-2.5=0.1，σ3=0.0167 ,则总长度之变异值为,,，总公差为0.248 明显比0.4小。

　　另解：依Pythagorean rule t2=a2+b2+c2+…..，a 、b 、c…，各件用平均偏差。AB段长度之变异(公差值)为2.5-2.4=0.1=6σ1 ，平均分配给最长与最短，

　　得σ1=0.0167 ,换言之;LAB =2.45±3σ=2.45±0.05，加工合格率为99.73%。而BC段长度之变异为3.2-3.0=0.2=6σ2 ,可得σ2=0.0333 ,或改为LBC =3.1±0.1。同理; CD段长度之变异为σ3=0.0167 , 或改为LCD =2.55±0.05，

　　则依统计原理，其总变异公差为,，,得σtotal =0.0412，则AD段长度之变异(公差值)为(8.3+7.9)/2 = 8.1±3σtotal=8.1±0.124，或。而统计公差0.248，明显比0.4小。

　　例.由4项零件组成之产品，各零件尺寸与公差如下图，求组合后之尺寸与公差？

图9. 4零件组成之产品示意图

解：组合尺寸平均值：，

　　组合最大尺寸：……（1），

　　组合最小尺寸：……（2），

　　组合偏差（1）－（2）：t=a+b+c+d………（3），与实务不符有落差，

　　假设a=b=c=d=0.02 mm，t=0.08 mm，

　　如依统计法，t=【4a²】^1/2=【4（0.02）²】^1/2=0.04 mm，

　　如依统计99.73％合格，σ1=0.02/3 mm，σ_t²=4σ₁²，σt=2σ₁=0.04/3 mm，t=3σ_t=0.04 mm。

　　反过来，如组合偏差t=0.04 mm，依累加法t=a+b+c+d均分，则a=b=c=d=0.01 mm，

　　如依统计法，t=【4a²】^1/2，a=b=c=d=t/2=0.02 mm，製作公差比直接累加法多 一倍，易製，费用降低，省时，彰显统计概念之优势。

　　例.由5支桿组成轴，首尾各长20.02 mm，中间3支长各为50.50 mm，每支之标準差均为0.01 mm，採随机法组立，依统计原理，求轴长平均值？标準差？轴长自然公差？轴长自然偏差？

解：轴长平均值：20.02×2+50.50×3=191.54 mm，

　　标準差：σ_t=（5×0.01）^1/2=0.022 mm，

　　轴长自然公差：6σ_t=0.132 mm，

　　轴长自然偏差：±σ_t=±0.066 mm。

　　得轴长191.54±0.066 mm。

　　例.依高度正确之製作之3项零件，各个尺寸统计均呈常态分布，随机各自3项零件各取一件线性组立，期望全长变化不超过±3σ_t=±4 mm，依累加法思维及统计原理求各项零件之製作偏差？

解：（1）依累加法思维：组合偏差±3σ_t=±4 mm，各项零件之製作偏差：±σ_t=±1.333 mm。

      （2）统计原理：σ_t²=σ₁²+σ₂²+σ₃²=3σ₁²，

　　ifσ₁=σ₂=σ₃，则σ₁=σ_t/(3^1/2)=0.769 mm，

　　各项零件之製作偏差：±3σ₁=±3（0.769）=±2.309 mm＞±1.333 mm，製作易，降成本。

　　由多项零件组立之机件，其组合尺寸之偏差设计，影响各零件之製作精度程度，考量因素：

　　1.组合尺寸功能需求。

　　2.各零件生产设备之製作精度。

　　3.其他相关设备之配合能力。

　　宜兼顾上述3项平衡且符合目前生产之经济原理，组合尺寸之偏差是否可由3σ放大至4σ。

(3)基準与基準尺寸

　　基準尺寸(Basic dimension BSC)：表示形体精确大小、形状与位置之理论值，做为对外尺寸或注解尺寸建立公差。如  。

图10. 基準与基準尺寸

　　指定某形态之位置度公差或轮廓度公差或倾斜度公差时，用于标注理论上正确之位置、轮廓或角度之尺度(尺寸)，是不加注公差，而是以尺度外加方框表示，该工件之相对应实际尺度仅受限于公差框内所标注之位置度公差或轮廓度公差或倾斜度公差，更非以未注公差比对或仅作参考。优点为：(1)弥补+/-公差之缺陷及不合理之处。(2)消除累积公差之困扰。(3)合理增大製作公差达57%以上。(4)配合MMC/LMC可再额外增大製作公差(Bonus tolerance/Zero tolerance)，大幅降低模具工具製作成本。(5)量产件之检具设计简单快速，提升研製效率与良率。

　　尺寸链标注其组合公差如採6σ之统计法，可获得较佳之公差值，比较允中。其他如採基线(Base line共同起点或面)标注，可得比尺寸链标注较少之累积公差。当然如採直接标注，其公差更比前述两种更小，但与配合件组合时将产生偏移问题，最佳法则建议引用几何公差(Geometric tolerance)之基準(Datum)与基準尺寸(Basic dimension BSC)标注，彻底消除累积误差变异。

(4) 间隙预估

影响组合公差因子：

　　(1)接触界面粗度问题、端面形状不平行、偏斜、瑕疵、防蚀镀层膜厚度等。

　　(2)组装线上人因工程简易、快速考量。

　　(3)市售机械设计CAD软体组立图有盲点，将零件图组合时採用界面与界面重叠，但工程实务上必有间隙产生，因此从CAD直接点选组合件之总长度必定比较实际组合件短一些。除非检测室量具归零时用块规从切面方向组合才无间隙。

　　(4)组件间隙预估，因各产品要求精度不一样，各产品需自行累积实务经验。

　　(5)组合件除长度计算时需加入间隙质外，尚需考量组合件之形状，可能不是理想中之真直，可能有些微弯曲、偏斜、扭曲、蜂腰、中广等现象，所以才有几何公差规範弥补这些缺陷，从零件管制起，尤其大量生产件更需俱全互换要求。

建议

　　欧美高科技国家已使用超过半世纪，并颁布规範(ISO 1101，ASME Y14.5，内容一致)供产业使用。JIS规範紧追ISO，只晚1~3年(专门机构引进，并编辑日文版供业界使用，并出英文版显示与国际同步)，充分与国际规範接轨，製作产品具相同功能甚至超越欧美规格，价格又比较低廉，产品才能打进欧美市场。国内机械产业(工具机、切削加工业、沖压板金业、射出塑胶业、模造橡胶业、粉末冶金业等)迎头赶上，认识、学习、消化、吸收、活用，急起直追，缩短技术落差，早日与老外产品拚搏于国际市场，取代日、韩抢占商机，增加外汇与获利，创造工作机会。

备注

　　１.Statistical tolerancing is the assigning of tolerances to related components of an assembly on the basis of sound statistics（such as the assembly tolerances is equal to the square root of the sum of the squares of the individual tolerances）. ASME Y14.5M （2.16） p.38 1994/p. 36~37 2009 。

　　2.60o螺牙面防蚀镀层如为一个单位厚度，则牙尖及牙谷增为两个厚度，公母螺牙组配时产生4个单位之厚度，造成干涉，很难锁到定位之最大原因。加工部门不可只要于完工后有组配到定位就交差，必需于防蚀工序完成后再次组配才是真正完工送验交货。